FxP-QNet: A Post-Training Quantizer for the Design of Mixed Low-Precision DNNs With Dynamic Fixed-Point Representation
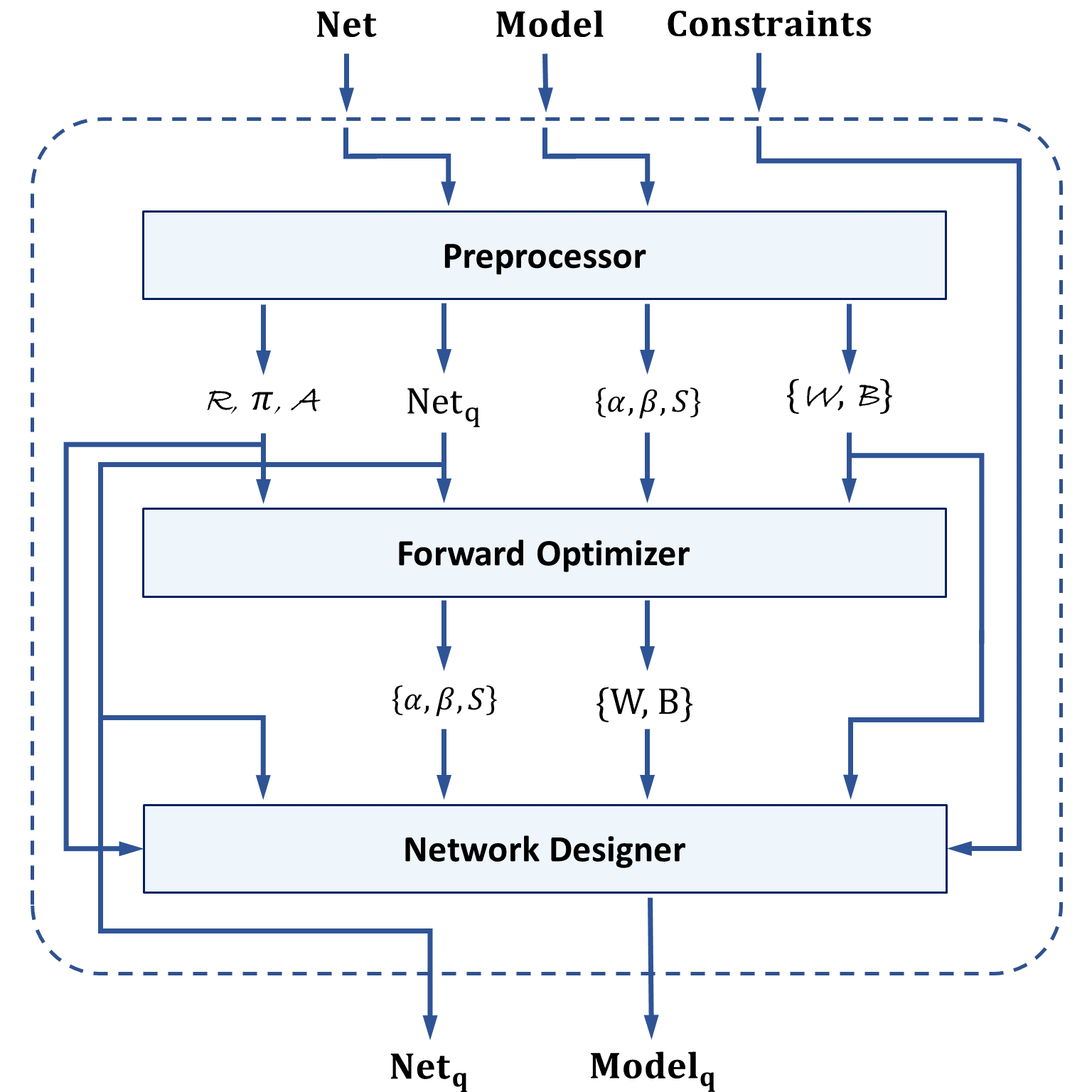
Deep neural networks (DNNs) have demonstrated their effectiveness in a wide range of computer vision tasks, with the state-of-the-art results obtained through complex and deep structures that require intensive computation and memory. In the past, graphic processing units enabled these breakthroughs because of their greater computational speed. Now-a-days, efficient model inference is crucial for consumer applications on resource-constrained platforms. As a result, there is much interest in the research and development of dedicated deep learning (DL) hardware to improve the throughput and energy efficiency of DNNs. Low-precision representation of DNN data-structures through quantization would bring great benefits to specialized DL hardware especially when expensive floating-point operations can be avoided and replaced by more efficient fixed-point operations. However, the rigorous quantization leads to a severe accuracy drop. As such, quantization opens a large hyper-parameter space at bit-precision levels, the exploration of which is a major challenge. In this paper, we propose a novel framework referred to as the Fixed-Point Quantizer of deep neural Networks (FxP-QNet) that flexibly designs a mixed low-precision DNN for integer-arithmetic-only deployment. Specifically, the FxP-QNet gradually adapts the quantization level for each data-structure of each layer based on the trade-off between the network accuracy and the low-precision requirements. Additionally, it employs post-training self-distillation and network prediction error statistics to optimize the quantization of floating-point values into fixed-point numbers. Examining FxP-QNet on state-of-the-art architectures and the benchmark ImageNet dataset, we empirically demonstrate the effectiveness of FxP-QNet in achieving the accuracy-compression trade-off without the need for training. The results show that FxP-QNet-quantized AlexNet, VGG-16, and ResNet-18 reduce the overall memory requirements of their full-precision counterparts by 7.16x, 10.36x, and 6.44x with less than 0.95%, 0.95%, and 1.99% accuracy drop, respectively.
